RTS10_verslagen/report-1/assambly_assignments.md

path	tags
/elektro/hr/rts10/	kladjes, elektro, elektro/hr, elektro/hr/rts10

parent

Assembly Assignment

This is the first report for realtime systems 10. I needed to do the following assignments:

• Assignment 1: Testing a simple LEGv7 Pinky program
• Assignment 2: Writing a simple multiplication program
• Assignment 3: A smarter multiply algorithm
• Assignment 10: Using your multiply function to calculate the dot product of two vectors

Assignment 1: Testing a simple LEGv7 Pinky program

First is getting a very basic example/base project to compile and run. The university supplied a zip file with a preconfigured project. I imported it into STM Cube IDE and tried to debug.

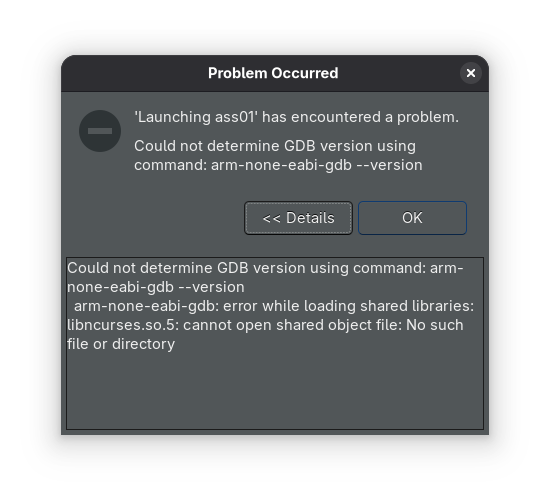
First I got a message to update the debugger firmware. After doing this, I still got an error. It could not determine the GDB version.

Last year I also had problems with GDB, but that time it was because it could not find the Windows version while I'm on Linux. Looking at the command, it does look like the usual Linux command. In the terminal this command is not found. After searching around on my system, I found it in the install directory from the IDE. Running the command on this executable gave the exact same error as the popup gave.

I have ncruses 6.5 installed, but version 5 is requested. I installed the older version and tried it again. Now I get the same error as last year.

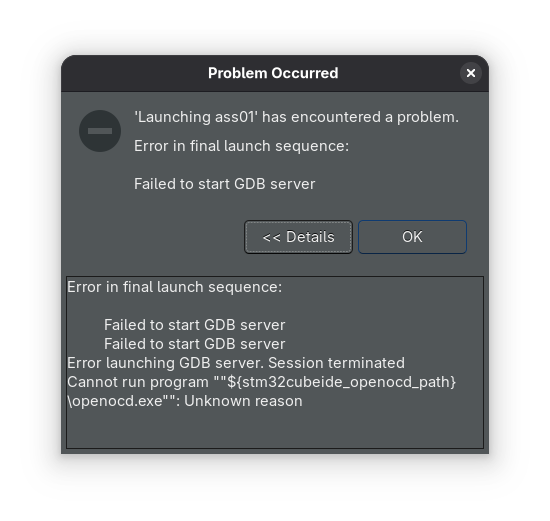
I applied the same fix as last year. In the debug config, replace the \ with an / and remove the .exe in the path to the OpenOCD command. This fixed the problem that the debugger successfully stated.

Assignment 2: Writing a simple multiplication program

The algorithm in question is given in C code.

unsigned int multiply(unsigned int a, unsigned int b)
{
    unsigned int m = 0;
    for (unsigned int i = 0; i != a; i ++)
    {
        m = m + b;
    }
    return m;
}

This code can be simplified without changing the algorithm by replacing the variable i with b. This will result in the following code.

unsigned int multiply(unsigned int a, unsigned int b)
{
    unsigned int m = 0;
    for (; b > 0; b --)
    {
        m = m + a;
    }
    return m;
}

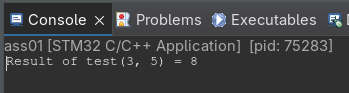
This is also the code I have implemented. The compiler puts a in R0 and b in R1, I accepted them in place and used R2 for m. At the end m (R2) is moved to R0 to set it as the return value.

    .cpu cortex-m4
    .thumb
    .syntax unified
    .globl multiply
    .text
    .thumb_func
multiply:
    MOVS.N R2, #0      // set m to 0
    CMP.N  R1, #0
    BEQ.N  mul_exit    // goto mul_exit if b == 0
mul_loop:
    ADDS.N R2, R0, R2  // add a to m
    SUBS.N R1, #1      // substract 1 from b
    BNE.N  mul_loop    // goto mul_loop if b != 0
mul_exit:
    MOVS.N R0, R2      // move m to R0
    BX.N   LR

a better representation of the essembly code in C would be:

unsigned int multiply(unsigned int a, unsigned int b)
{
    unsigned int m = 0;
    if (b == 0) {
      return m;
    }

    do
    {
        m = m + a;
        b --;
    } while (b > 0)

    return m;
}

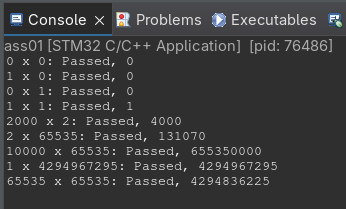
How many instructions does it take your procedure to run the code: multiply(65535, 65535)?

It does not take the branch at line 10 and at line 14 it takes the branch 65535 times. There are 3 instructions in this loop and 5 outside it, so 3\cdot 65535 + 5 = 196610 instructions.

Assignment 3: A smarter multiply algorithm

Now a smarter version.

unsigned int multiply(unsigned int a , unsigned int b)
{
    unsigned int m = 0;
    while (b != 0)
    {
        if ((b & 1) == 1) /* b is odd */
        {
            m = m + a;
        }
        a = a << 1;
        b = b >> 1;
    }
    return m;
}

    .cpu cortex-m4
    .thumb
    .syntax unified
    .globl better_multiply
    .text
    .thumb_func
    // R0 = a, R1 = b, R2 = result (m), R3 = bitmask or odd/even bit
better_multiply:
    MOVS.N R2, #0      // set m to 0
    CMP.N  R1, #0
    BEQ.N  bmul_exit   // goto bmul_exit if b == 0
bmul_while:
    MOVS.N R3, #1      // set R3 to 1 as bit mask
    ANDS.N R3, R1      // and R3 (bit mask) with b
    BEQ.N  bmul_even   // goto even if result is 0
    ADDS.N R2, R0      // add a to m
bmul_even:
    LSLS.N R0, R0, #1  // a = a << 1
    LSRS.N R1, R1, #1  // b = b >> 1
    BNE.N  bmul_while  // goto while if b != 0
bmul_exit:
    MOVS.N R0, R2      // move m to R0
    BX.N   LR

a better representation of the essembly code in C would be:

unsigned int multiply(unsigned int a, unsigned int b)
{
    unsigned int m = 0;
    if (b == 0) {
      return m;
    }

    do
    {
        unsigned int t = 1;
        if ((b & t) != 0) {
            m += a;
        }
        a = a << 1;
        b = b >> 1;
    } while (b != 0)

    return m;
}

How many instructions does it take your procedure to run the code: multiply(65535, 65535)?

There are 7 instructions in the loop where one only runs every 1 bit in b. The loop only runs every bit in b until it's zero. In this case b is 65535 or 16 ones in a row in binary. The full 7 instructions run 16 times plus the 5 instructions outside the loop. In total it's 16\cdot 7+5=117 instructions. This is about 1680 times less instructions than the other algarium.

Assignment 10: Using your multiply function to calculate the dot product of two vectors

unsigned int dotProduct(unsigned int a[], unsigned int b[], size_t n)
{
    unsigned int p = 0;
    for (size_t i = 0; i != n; i++)
    {
        p = p + multiply (a[i], b[i]);
    }
    return p;
}

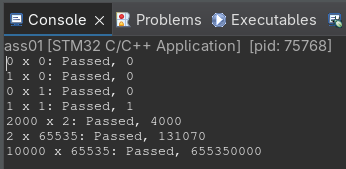
This function needs to call another and remember 5 variables (*a, *b, n, p and i). R0 through⁣ R3 are expected to change with a function call. There are only R4 through R7 left, only four spots. To solve this problem, I reversed the for loop by using n and decrementing it. This will not change the result since addition is not order sensitive. The code I implemented is the following.

unsigned int dotProduct(unsigned int a[] , unsigned int b[], size_t n)
{
    unsigned int p = 0;
    if (n == 0) {
        return p;
    }
    unsigned int i = n;
    do
    {
        i--;
        p = p + multiply(a[i], b[i]);
    } while (i != 0)
    return p;
}

My assembly code:

    .cpu cortex-m4
    .thumb
    .syntax unified
    .globl dot_product
    .text
    .thumb_func
    // R4 = a, R5 = b, R6 = i, R7 = p (result)
dot_product:
    PUSH.N  {R4, R5, R6, R7, LR}
    MOVS.N  R4, R0      // move *a to R4
    MOVS.N  R5, R1      // move *b to R5
    MOVS.N  R7, #0      // set p to 0
    MOVS.N  R0, R2      // move n to R0
    MOVS.N  R1, #4      // set R1 to 4
    BLX.N   =better_multiply // n * 4
    MOVS.N  R6, R0      // move result to R6
dotp_loop:
    SUBS.N  R6, R6, #4  // i = i - 4
    LDR.N   R0, [R4,R6] // load a[i] to R0
    LDR.N   R1, [R5,R6] // load b[i] to R1
    BLX.N   =better_multiply
    ADDS.N  R7, R7, R0  // p = p + result
    BNE.N   dotp_loop   // goto dotp_loop if i != 0
dotp_exit:
    MOVS.N  R0, R7      // move m to R0
    POP.N   {R4, R5, R6, R7, PC}